Table of Contents
Simple Harmonic Motion and Mechanical Resonance - PHYS141
You will work with a complex system to do the following:
- look at the effects of driving and damping forces on a simple harmonic oscillator,
- explore the general features of mechanical resonance, and
- measure characteristics of our resonant system such as the amplitude-vs-frequency resonance curve and the Q-factor.
Introduction
Simple harmonic motion is motion which results from a Hooke's law force,
| $\textbf{F} = -k\textbf{x}$, | (1) |
and such motion is described by the function
| $x(t) = A\cos(\omega_0 t + \delta)$ | (2) |
where $A$ is the amplitude, $\delta$ is a phase, and $\omega_0$ is the natural frequency,
| $\omega_0 = \sqrt{k/m}$. | (3) |
Today we will investigate how the equations of motion change when we add additional forces – damping forces of the form $\textbf{F} = -b\textbf{v}$ and sinusoidal driving forces of the form $\textbf{F} = \textbf{F}_0 \cos \omega t$.
Apparatus
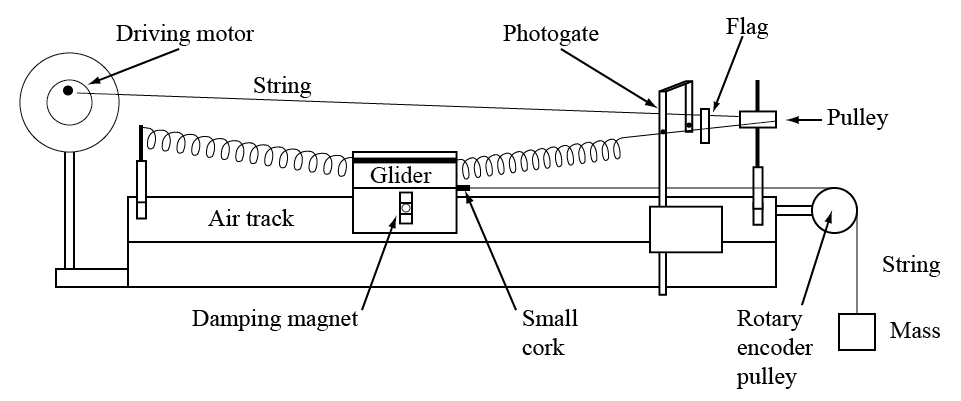
The oscillating system we will use today consists of a glider with attached springs on an air track (see Fig. 1). The air track provides a cushion of air which reduces friction on the cart, allowing us to more easily visualize the motion due to the other forces acting on the mass.
Let's discuss the more important parts of this system.
- The glider is a metal cart designed to float on top of the air cushion of the air track. It is the main component of the total mass that we will oscillate.
- The springs are attached to the glider by looping over the rubber band around the top of the glider.
- The driving motor can be used to turned at an adjustable frequency to add a sinusoidal driving force.
- The photogate timer is an electronic stop watch.
- We will use this device in “pendulum” mode such that it will measure the period of the flag on the string as the motor pulls the string back and forth.
- The rotary encoder is connected to a LabQuest Mini USB device which is in turn connected to the computer.
- Just like in part 1, we can pass a mass clip hanging on a string over the rotary encoder pulley and use the rotation of the pulley to measure displacement as a function of time in software.
- The string is attached to the glider with a cork shoved into a hole at the base of the glider.
- The damping magnets are used to apply (or remove) a damping force to our cart.
- When they are placed with their poles facing down towards the air track, they will produce eddy currents in the metal of the track, damping the motion.
- When they are placed with their poles facing up away from the air track, they do not produce any damping force.
Lab notebook
Google Colab notebook
To help visualize and fit your data, we provide a Google Colab notebook.
Experimental procedure
Characterizing your system
In Part 1, you measured the mass, spring constant, and period of a single mass and single spring system. Today, you will repeat this procedure, but for the more complex system consisting of two springs attached to a glider (which is also attached to a string and hanging mass clip which move along with it).
Set the apparatus as shown in Fig. 1. Attach one spring to each end of the glider using the rubber band. Cut a string to about 1.5 meters in length and secure one end of the string in the lower end-hole of the glider using a small cork. Pass the string over the rotary encoder pulley and attach one small mass clip to the free end. Note where the glider is currently sitting. This will be the equilibrium position of the glider.
Turn on the blower to provide air to your air track. Open the SHM configuration file on the desktop and check to make sure the rotary encoder is working by recording some data as you move the cart around.
If the file isn't there, or if you need a fresh, unedited copy, it is available to download here: shm.cmbl.
Your tasks are the following:
- Measure the mass.
- Determine the spring constant.
- Calculate the expected natural frequency (or period) of oscillation.
- Measure the natural frequency (or period) of oscillation of the system.
- Try to measure the frequency for both the case of magnets down (providing damping) and up (providing no damping). (You may or may not notice a difference. Comment on what you see.)
- Compare you predicted and measured frequency values.
Below is some advice that may be useful.
Mass
The “mass” which will be oscillating in this experiment is a metal glider plus the rubber band, the two magnets, the cork, the string, and the single mass clip attached to the string.
- Carefully detach the springs from the glider (leaving the rubber band on).
- Leave the two magnets attached, along with the cork, string and one mass clip.
- Don't forget to estimate uncertainties!
Spring constant
You can use a similar technique to determine the spring constant as you did last week: looking at the displacement of the mass as a function of force (due to hanging additional weight on the string).
- Remember that one mass clip is included in the mass you measured above, so don't count that one as additional weight!
- Use the position of the glider at rest (with one mass clip on the string) as your equilibrium point.
Period
You will want to measure the period, $T$ (or equivalently, the angular frequency, $\omega = 2\pi/T$) for the system in two case: with both magnets are pointing up and with both magnets pointing down.
- There are multiple ways to measure the period or frequency… the method is up to you.
- Depending on your technique, you may or may not find any difference between the frequency when the magnets are up or down. That's OK.
- Don't forget to estimate uncertainties.
Damped harmonic motion
If, in addition to a Hooke’s Law restoring force, a damping force is also applied to the oscillating object, the resulting motion will change. Many damping forces may be represented by
| $\textbf{F} = -b\textbf{v}$, | (5) |
(i.e., by a force proportional to the velocity of the object, directed oppositely to its direction of motion) where $b$ is the damping constant. With damping included, the equation of motion is
| $m\dfrac{d^2x}{dt^2} + b\dfrac{dx}{dt} + kx = 0$, | (7a) |
which can be rewritten as
| $\dfrac{d^2x}{dt^2} + 2\xi\dfrac{dx}{dt} + \omega_0^2 x = 0$, | (7b) |
where we introduce the damping ratio,
| $\xi = \dfrac{b}{2m}$. | (8) |
This function has different solutions depending on the magnitude of $\xi$. Today, our system will be underdamped (meaning $\xi < \omega_0$). The solution to the equation in this case is given by
| $x(t) = A e^{-\xi t}\cos(\omega^{\prime} t + \delta)$, | (9) |
where $A$ is the initial amplitude of oscillation, $\delta$ is the initial phase of the oscillation, and $\omega^{\prime}$ is the new damped oscillation frequency,
| $\omega^{\prime} = \sqrt{\dfrac{k}{m} - \bigg(\dfrac{b}{2m}\bigg)^2} = \sqrt{\omega_0^2 - \xi^2}$. | (10) |
Hence, we see that the damped frequency is less than the natural frequency $\omega_0$.
A plot of Eq. (9) is shown in Fig. 2. (This should look familiar from Part 1! Your simple mass on a spring system was an underdamped system.)
Observing damped oscillation
In order to quantify our damped oscillatory motion, we want to make a few measurements.
First, with the magnets down (i.e. with damping), do the following:
- Pull your glider away from equilibrium and release.
- Start collecting data on the software. Allow the mass to go through many oscillations so that the amplitude decreases with time before stopping collection. (You don't have to let the mass come completely to stop.)
- Fit the displacement data to the Damped Harmonic function in the software*.
- What is the value of $\xi$ you find?
- Are we in fact in the underdamped regime where $\xi < \omega_0$?
- Using this value of $\xi$, what is the damped frequency, Eq. (10)? Is this consistent with what you measure from the software?
*From the Analyze menu, select Curve Fit. In the General Equation list box, select Damped Harmonic. In the equation that appears, the meaning of the constants are as follows:
- $A$ is the amplitude of the wave, $A$;
- $B$ is the damping ratio of the exponential, $\xi$;
- $C$ is the frequency of oscillation, $\omega = 2\pi f$;
- $D$ is the phase, $\delta$; and
- $E$ is the vertical offset (which is not included above in Eq. (9) above, but which accounts for the fact that rotary encoder measures displacement from the position at $t=0$, not distance as marked on the ruler on the front of the air track.)
Now, repeat the above for the situation where the magnets facing up. This will remove the damping force due to the eddy currents, but there are still small frictional forces at play (so we aren't quite at a point of “zero damping”, but we can at least say we are “less damped” than before.)
- What is the value of $\xi$ you find this time?
- Is it bigger or smaller than in the damped case where the magnets face down? Is that what you expect?
- Using this value of $\xi$, what is the damped frequency, Eq. (10)? Is this consistent with what you measure from the software?
Forced and damped harmonic motion: Resonance
Suppose now we add to the damped oscillator a periodic driving force of the form
| $\textbf{F} = \textbf{F}_0 \cos (\omega t)$, | (11) |
where $\omega$ is the frequency of the driving force and $\textbf{F}_0$ is the amplitude of the driving force.
Adding this force to the Hooke's law restoring force and the damping force we find a total equation of motion
| $m\dfrac{d^2x}{dt^2} + b\dfrac{dx}{dt} + kx = F_0 \cos(\omega t)$ | (12a) |
or
| $\dfrac{d^2x}{dt^2} + 2\xi\dfrac{dx}{dt} + \omega_0^2 x = \dfrac{F_0}{m}\cos(\omega t)$. | (12b) |
The solution to this differential equation is complicated at early times, but if we wait long enough for the transient behavior to die out, then the long time steady solution is
| $x(t) = A_D \cos(\omega t + \phi)$, (for $t \gg 0$) | (13) |
where the amplitude $A_D$ is given by
| $A_D = \dfrac{F_0/m^2}{\sqrt{(\omega_0^2 - \omega^2)^2 + 4\xi^2\omega^2}}$ | (14) |
and the phase is given by
| $\phi = \tan^{-1}\bigg[\dfrac{2\xi\omega}{(\omega^2 - \omega_0^2)}\bigg]$. | (15) |
Equation (14) tells us that for constant amplitude driving force $F_0$, the amplitude of the oscillation is a function of $\omega$. In particular, it tells us that the amplitude of oscillation has a maximum when $\omega = \omega_0$, i.e., when the driving frequency is in resonance with the natural frequency. It also tells us that if there were no dissipative forces ($b=0$, or equivalently, $\xi = 0$), then the amplitude would go to infinity at the resonant frequency no matter how small the driving force!
A plot of Eq. (14) is shown in Fig. 3 for different values of damping coefficient, $\xi$. As should be apparent from this figure, the amplitude of the oscillation at resonance is higher than at any other frequency, and the magnitude of the resonant oscillation gets larger as $\xi$ gets smaller.
The phase angle $\phi$, Eq. (15), specifies the time relationship between the driving force and the resultant displacement as a function of $\xi$, the driving frequency $\omega$, and the natural frequency $\omega_0$. A plot of phase angle versus driving frequency is shown in Fig. 4.
We see the following from the figure:
- When the driving frequency is much less than the resonant frequency, the phase of oscillation is the same as the phase of the driving force: $\phi \rightarrow 0^{\circ}$.
- When the driving frequency is much greater than the resonant frequency, the phase of oscillation is completely opposite the phase of the driving force: $\phi \rightarrow -180^{\circ}$.
- When the driving frequency is equal to the the resonant frequency, the phase is $90^{\circ}$ out of phase with the driving force: $\phi = -90^{\circ}$.
Observing "damped" resonance
For the following measurements, we shall use the magnets, mounted on the glider mass pins, with their pole faces pointing down toward the air track.
Turn on the motor and observe the behavior of the glider as you adjust the frequency.
- For a range of driving frequencies around the natural frequency, measure and plot the glider's amplitude as a function of driving frequency. Note that for each change in the driving frequency you must wait long enough to allow the erratic (transient) motions to die out before measuring the amplitude.
- Estimate uncertainty on both frequency (or period) and amplitude.
- Measure enough data to plot out the full range of interesting features – some points far below resonance, some points far above resonance, and lots of points around resonance.
- Also, observe (but do not measure) the phase of the oscillations when you are far below, far above, and near resonance.
- Do they qualitatively agree with the plot shown in Fig. 4?
Observing "undamped" oscillations
Re-orient the magnets with their pole faces pointing away from the track.
Tune the driving frequency for maximum amplitude of the glider.
- Comment on your observations.
NOTE: You do not need to measure and plot the full resonance curve for the undamped case (though there is a place within the Google Colab to do so if you want!)
Quality factor, $Q$
The quality factor, $Q$, of an oscillating system is a measure of how many oscillations will take place before the motion dies out. There are several ways to express the $Q$ of an oscillating system.
In terms of energy, we can define $Q$ as
| $Q = 2\pi \dfrac{\textrm{energy stored in the system}}{\textrm{energy lost per cycle}}$. |
In terms of amplitude, we can define $Q$ as
| $Q = \dfrac{\textrm{amplitude at resonance}}{\textrm{amplitude at small driving frequency}}$. |
But, the definition we will use for our system today is the definition revolving around the width of the resonance peak:
| $Q = \dfrac{\omega_0}{\Delta \omega}$ |
where $\Delta \omega$ is the full width at half maximum (FWHM) of the peak (as shown in Fig. 4).
 |
| Figure 4: The full width at half maximum of a curve is the distance (along the $x$-axis) between the two points where the amplitude is half the maximum value (along the $y$-axis). (Source: Wikipedia) |
The full width at half maximum is related to the damping factor as
| $\Delta \omega = 2\xi$ |
such that
| $Q = \dfrac{\omega_0}{2\xi}$. |
- Estimate the full width at half maximum, $\Delta \omega$, from your damped resonance curve. (There is no need to estimate uncertainty.)
- How does your measurements compare to the value of $2\xi$ (using the value found from the Logger Pro fit of the motion in the damping-only section above)?
- Using $\omega_0$ and $\Delta \omega$, calculate $Q$.
Submit your lab notebook
Make sure to submit your lab notebook by the end of the period. Download a copy of your notebook in PDF format and upload it to the appropriate spot on Canvas.
Don't forget to log out of both Google and Canvas, and to close all browser windows before leaving!