Table of Contents
Atomic and molecular spectra and applications in oximetry
This will be a two week lab. In the first week, we will be using the principles of diffraction to study the absorption and emission spectra of atomic gases. We will then see in the second week how analyzing the absorption spectrum of a substance can be of great use and importance in medicine and biosciences. In particular, you will develop your own “oximeter”, an important apparatus used in medicine to measure the saturation of oxygen in hemoglobin to monitor a patient’s health.
Learning goals
By doing this experiment, you will:
- use a diffraction grating spectrometer to study the emission spectra of atomic gases;
- identify an unknown gas by its emission spectrum;
- develop and apply a physical model of light transmission in medical technologies;
- explore the concept of relative measurements through the Beer-Lambert law and use it to determine concentrations of substances in a solution.
Diffraction
The term interference describes wave phenomena originating from a small number of point sources. (By a point source we mean a source of waves having linear dimensions small in comparison to the wavelength of the radiation.) The term diffraction applies to the spreading of waves at apertures and can be thought of as resulting from the interference of many coherent point sources. Sources are coherent when they oscillate with a phase relationship that does not vary in time.
Suppose now instead of a point source we consider an extended source, i.e., a source larger than the wavelength under consideration. Such a source can be considered as a large array of coherent point sources and from our definition of diffraction it should be clear that waves from such a source should exhibit diffraction effects.
In the first part of this experiment, we will be using the principles of diffraction to study light spectra. In particular, we will be using a diffraction grating spectrometer to observe the emission lines of different atomic gases and identify the gases based on these lines.
Diffraction Theory
Before getting into the specifics of emission spectra and the diffraction grating spectrometer, it may be worthwhile to refresh your memory on interference and diffraction. The important results will be highlighted in the text that follows.
Interference from two point sources
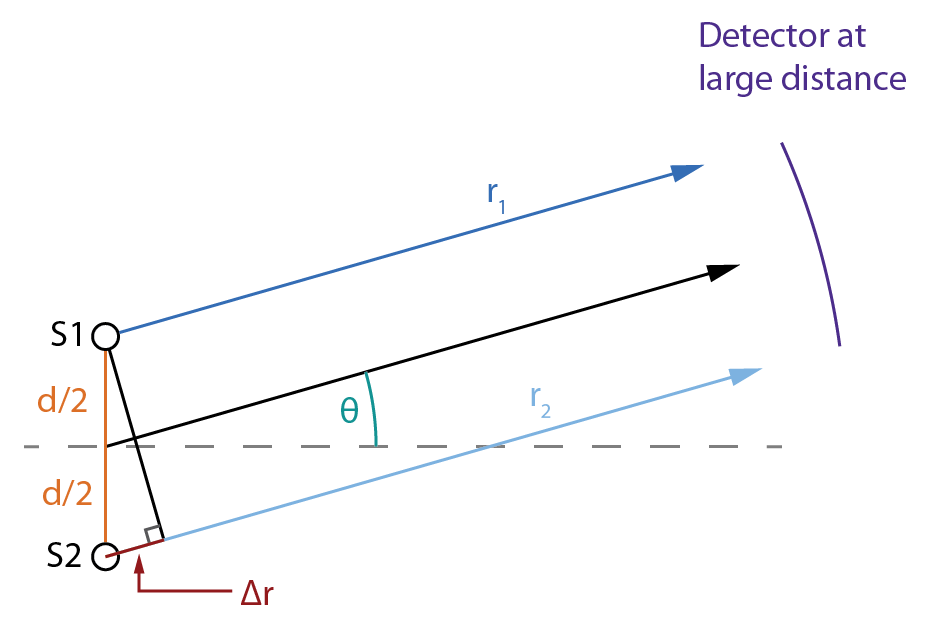
Figure 1 represents the wave disturbance originating from two point sources, S1 and S2, separated by a distance $d$. By the superposition principle, the intensity observed at the detector will be a maximum (i.e., the waves will be in phase) if the path difference, $\Delta r = r_2-r_1$, is an integral number of wavelengths, i.e. $\Delta r = n\lambda$. But, for a detector far from the sources, $\Delta r = d\sin\theta$. Therefore, the angles at which the intensity will be a maximum, denoted by $\theta_{max}$, obey the following relation:
| $n\lambda = d\sin\theta_{max} (\mathrm{for\;n = 0,1,2,\dots)}$. | (1) |
The intensity observed at the detector will be a minimum if the two sources are out of phase, i.e., $r = \left(n + \frac{1}{2}\right)\lambda$. Therefore, denoting angles where we expect an intensity minimum by $\theta_{min}$, we have
| $\left(n+\dfrac{1}{2}\right)\lambda = d\sin\theta_{min} (\mathrm{for\;n = 0,1,2,\dots)}$. | (2) |
Single slit diffraction
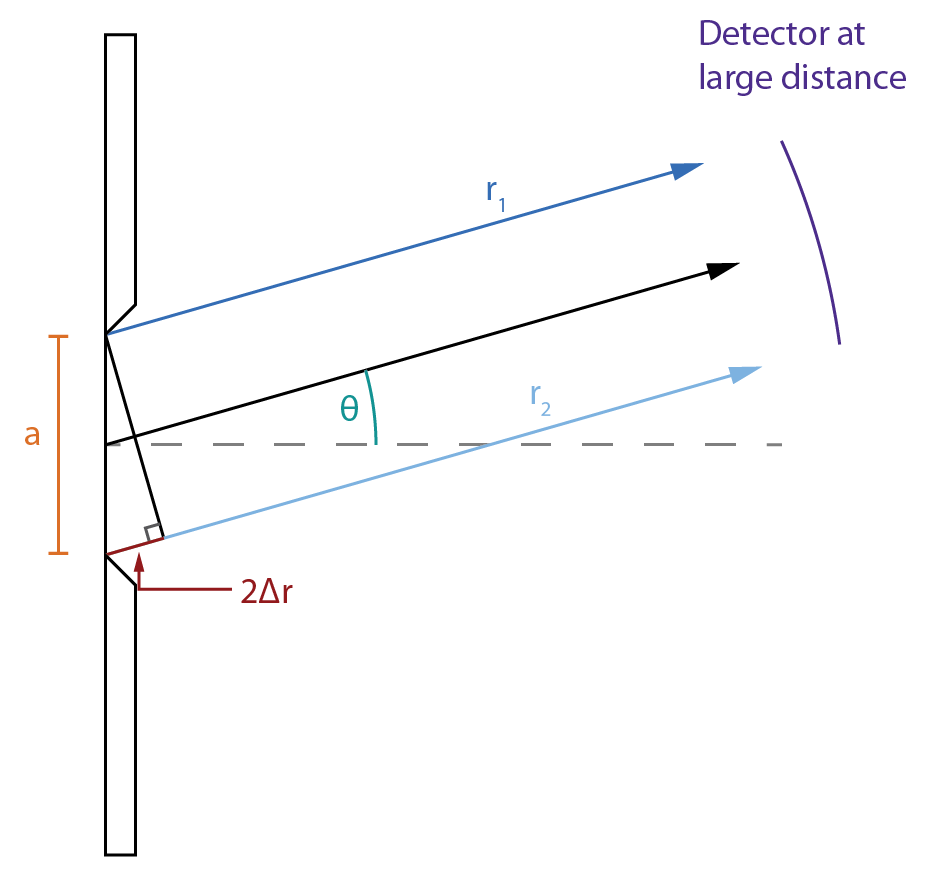
Now, consider an extended source, e.g., a slit, having width $a$ as shown in Fig. 2. We can consider the pattern of diffracted light coming from such an extended source as that resulting from the interference pattern of an infinite number of point sources within the slit, all oscillating in phase.
To find the angles where the intensity will be a minimum, let us divide the extended source of width $a$ into two equal regions: the top and bottom halves of the slit. Now suppose that we are at such an angle $\theta$ that the path difference between a source at the top of the slit and one at the middle of the slit is exactly one-half wavelength; then it is clear that these two will cancel and give no contribution at the detector. Also, it should be clear that the contribution from the entire slit will as well be zero at this angle. This is because for any source in the top half of the slit, we can find one in the bottom half (namely one a distance $a/2$ from the upper source) which will, when added, give zero intensity. Thus, our condition for a minimum intensity becomes
| $\Delta r = \dfrac{a}{2}\sin\theta_{min} = \dfrac{n\lambda}{2}$ (for $n = 1,2,3,\dots$). | (3) |
(Note that $n=0$ is not included.) Thus,
| $a\sin\theta_{min} = n\lambda$ (for $n = 1,2,3,\dots$). | (4) |
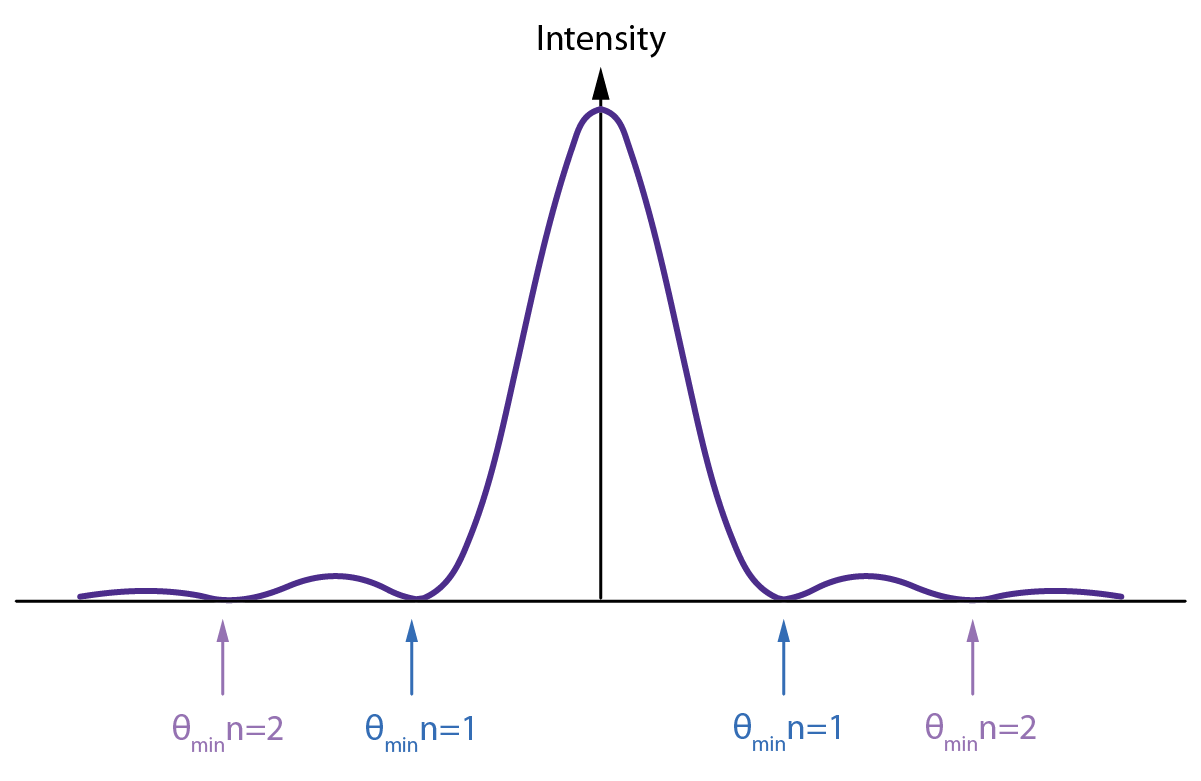
The maxima will occur approximately halfway between the minima. A single slit diffraction pattern is shown in Fig. 3.
Two slit diffraction
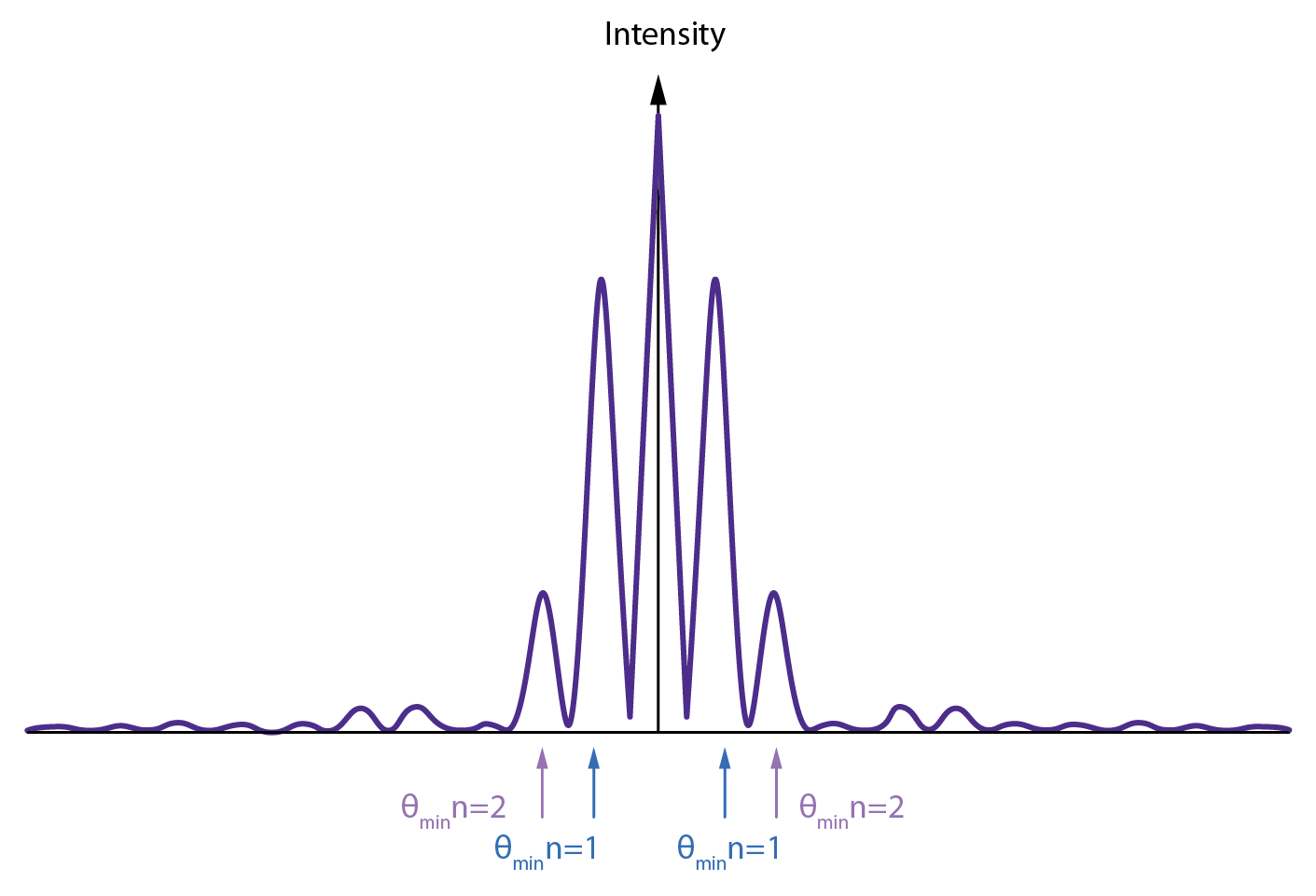
The pattern of transmission through two slits will depend upon both the width of the slits and their spacing. The amplitude from either slit at angle is governed by the single slit diffraction pattern - whereas the intensity from the two interfering slits will depend upon the interference pattern from two point sources. An intensity pattern similar to that shown in Fig. 4 will result. Note that the two slit pattern of Fig. 4 would lie entirely beneath the single slit pattern of Fig. 3, showing that the larger scale shape of the two slit pattern is still dictated by the widths of the individual slits.
Three slit diffraction
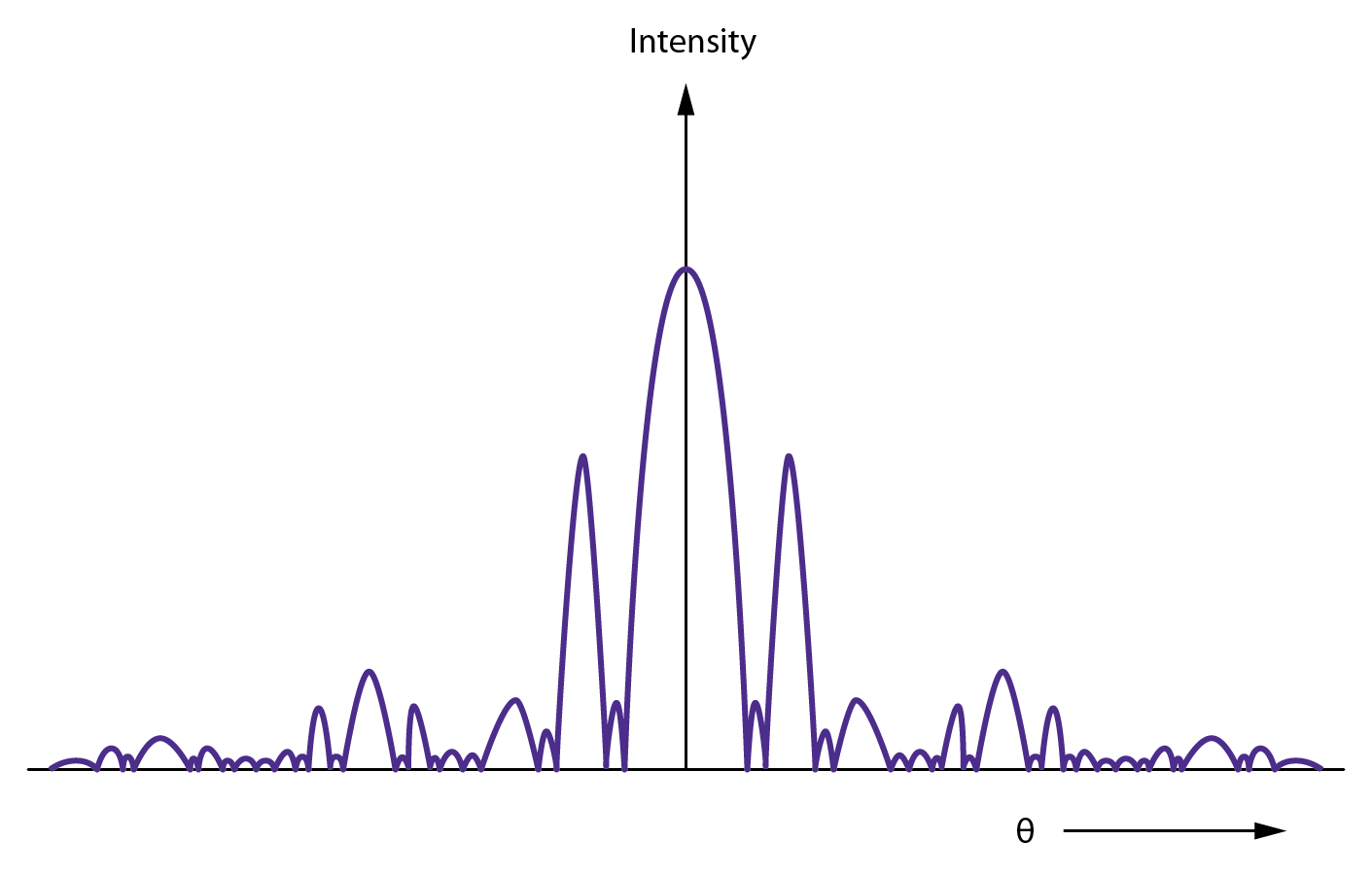
Consider the interference pattern produced by three slits. Slits 1 and 2 together would act as a double slit and therefore produce the first minimum given by Eq. (4). Slits 2 and 3 alone would produce a minimum at exactly the same angle. However, the pattern from the slits 1 and 3 will actually produce a (secondary) maximum at the above angle. The overall amplitude at this angle will be one-third the amplitude from that of the diffraction envelope, because two of the slits cancel each other out. So, the intensity at this angle (a minimum in the two slit pattern) will be one-ninth of the diffraction envelope and will be a maximum.
Fig. 5 depicts the intensity pattern from such a three-slit arrangement. Note that the intensity goes to zero on each side of the secondary maximum.
Multiple slit diffraction
The point that we wish to stress here is that when we add a third slit to our two slit arrangement, the position of the first minimum moves closer to zero. As a result, the central maximum becomes narrower. For similar reasons, the maxima in all orders become increasingly narrow as we add more slits. It can be shown that the angular width of the peaks is inversely proportional to N, the number of slits. Thus, the resolution of a slit system, which is its ability to separate two closely spaced wavelengths, is proportional to N.
Diffraction grating
As noted in the foregoing discussion, the resolution of a slit system increases with increasing number of slits. In the limit as the number of slits gets large, the central maximum of the diffraction pattern becomes narrower. For light normally incident on an equally spaced set of slits (as in Fig. 6), the relation among the diffraction angle $\theta$, the slit separation $d$, and the wavelength of the light $\lambda$ is given by
| $n\lambda = d\sin\theta_{max} (\mathrm{for\;n = 0,1,2,\dots)}$. | (5) |
If we solve for $\theta_{max}$ in the above equation, we see that $\theta_{max} \propto \text{arcsin}(\lambda)$, meaning that light of longer wavelengths will be diffracted at larger angles than light of shorter wavelengths. This makes diffraction gratings an excellent tool for measuring wavelengths. More specifically, is we send polychromatic light consisting of a distribution of wavelengths through a grating, we can separate the light into its constituent wavelengths. The angles at which they are diffracted, along with the diffraction order $n$, and the grating spacing $d$, will give us information about the wavelengths in the light.
In the image below you can see what a diffraction grating does to a polychromatic, or white, light source such as sunlight coming from the windows into the room. Just as equation 5 predicts, shorter wavelengths (blue) diffract at smaller angles than longer wavelengths (red), so that the blue bands are closer to the window than the red bands are. Also note that higher order diffraction maxima for shorter wavelengths can overlap with the lower order maxima of longer wavelengths.
Absorption and emission spectra and diffraction grating spectrometers
From the above discussion, we can see that the diffraction grating is an excellent tool for separating light into its constituent colors. In fact, they are commonly used in spectrometers to make precise measurements of wavelengths and are what allowed the discovery – or rather the quantitavie observation – of the emission and absorption spectra of gases in the eighteenth century. Scientists then observed that, when certain metals and salts are burned, they emit a flame with a specific color unique to the material that was burned. Similarly, gases that are subjected to a high electric field – that is, when we run a current through them –, emit light of a specific color, such as the characteristic red lighting of neon lamps. These gases were also observed absorbing the same colors of light that they emitted while transmitting other colors. By using a diffraction grating, they could see that the light emitted by these substances consisted of individual colors instead of a continuous distribution of wavelengths, which would prove to be an important observation for the development of quantum theory.
The figure below shows what we mean by emission and absorption lines.
Where do these lines come from?
While we will be working with absorption and emission spectra during this experiment, it is not necessary to fully understand the theory behind these spectra to gain some physical insight into the systems we're considering or even do some interesting applications. In fact, to fully understand the origins of the phenomena we'll study, we need the tools of quantum mechanics, which are beyond the scope of this course. However, it may be useful to have the basic mechanisms that give rise to these lines on the back of your mind.